운동방정식(미분방정식)의 수열의 합을 통한 응용에 대해서
프로그래밍 2006/07/15 12:32 미분방정식의 수열의 합을 통한 응용에 대해서
http://www.xevious7.com/103 2006년 7월15일.
오래전에 점프나 포탄의 움직을 컴퓨터화면에 표시하기 위해서 직관적인 방법으로
사용했던 알고리즘을 한번 수학적으로 생각해보고 정리한 문서입니다.
직관적인 생각의 전개는 http://www.xevious7.com/102
에서 볼 수 있습니다. (즉 대략 직관적으로 저렇게 해도 비슷한 곡선이
나올것 같았고 실제로 해보니 그런곡선이 나오더라 에서 근데 왜 비슷한
곡선이 나오지 하고 이유를 생각해본 문서라고 할까요 ~)
이유를 생각해보니 단순하게 증분을 더하는 형태이고 .. 증분이 1일때
결국 1에서 n까지의 수열합으로 표시될 수 있었습니다.
즉 위의 방법은 n(n+1) / 2 의 형태의 운동방정식이 되는 것입니다.
그래서 생각한것이 그럼 일반 운동방정식 a * n^2 + c 형태의 방정식도 수열합이 가능하지
않을까 라고 생각해서보니 일반항이 2*n -1 인 수열의 합이 n^2 이므로 이것도 더하는
값만 n에서 2*n -1 으로 바뀐 똑같은 알고리즘 적용이 가능하다는 것까지 생각했습니다.
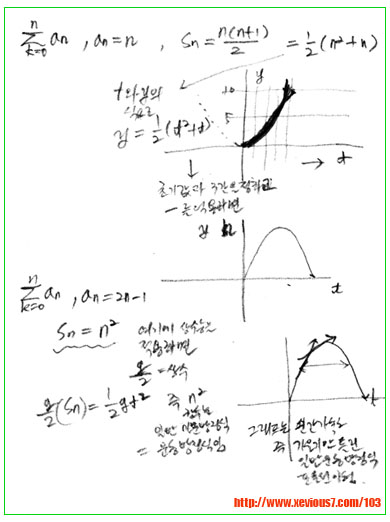
시간이 일정하고 시간의 값이 불변할때 이미 뉴튼에 의해서 이미 증명된 운동의방정식은
참입니다. 위의 글의 방법을 수열로 표현하면
즉 일정구간 (일정시간) T에 관한 거리는 각각 구간의 합으로 표현될 수 있다.
라는 것입니다.
좀더 이해를 이해서 풀어쓰면
T =1 일때 S1 = 1
T =2 일때 S2 = 1 + 2
T =3 일때 S3 = 1 + 2 + 3
T = n일때 Sn = 1 + 2 + 3 .... + n 이 됩니다.
이것은 일반항 An = n 인 수열의 합이 됩니다. 이 수열의 합은 수학교육과정에서
가장 먼저나오는 1에서 임의수 n까지의 정수합은 얼마인가? 라는 문제이고
알다시피 1/2 * n * (n + 1) 이며 이것은 2차방정식으로 운동의 방정식이 됩니다.
여기까지는 이미 대략적으로 전글에서도 알수 있는 것이지만 좀더 수학적으로
정리해보았습니다.
그런데 우리가 알고 있는 실제 운동의 방정식은 s = a * t ^2 의 꼴입니다.
위에서 2차 방정식이 수열의 합으로 표현하여 식을 간단히 했듯이 위의 운동방정식도
s값을 수열의 부분합이라고 생각하면 그 합이 n^2 이 된다고 생각할 수 있습니다.
다행히도 부분합이 n^2 을 가지는 수열은 잘 알려진 일반항이 An이 2n - 1 인
수열의 합이 됩니다.
이것을 이해하기 쉽게 풀어보면
T = 1 일때 S1 = 1
T = 2 일때 S2 = 4 = 1 + 3
T = 3 일때 S3 = 9 = 1 + 3 + 5
T = n 일때 Sn = n^2 = 1 + 3 + 5 + .... + 2n+1 이 됩니다.
자 이러면 우리가 현실세계의 사용하는 실제 운동의 방정식도 시간의 길이가 불변하는
일정구간 T에 대해서 곱을 사용하지하고 합을 사용하여 간략하게 표현할 수 있습니다.
즉 한번의 T구간에 대해서
거리는 부분합이므로
컴퓨터 알고리즘에서는 For 문에서 일반항만 계속 더하는 형태로
부분합을 구하면 그것이 바로 우리가 원하는 거리가 되는 것입니다.
즉 Tn 시점에서의 거리는 Tn-1 시점의 거리 + 일반항 이면 족합니다.
이렇게 미분방정식으로 수열로 생각하여 알고리즘을 구성하는 것은 여러응용에
훨씬 도움을 주리라고 생각합니다.
PS. 위의 방정식들을 보시다 시피 n(n+1)/2 나 n^2 의 기하학적인 곡선은 거의
동일하다고 생각할 수 있습니다. 왜냐면 n^2 를 1/2 로 스케일링 하면 큰 차이가
없는 곡선이 되는것입니다. 또한 그 곡선자체가 컴퓨터 그래픽에서 표현되는것이라면
사실상 무시해도 전혀 지장이 없습니다. 시뮬레이션이 아니라면 말이죠
따라서 1씩 증가하는 패턴의 공식으로 점프의 높이를 구현하는것이 속도상 조금의
이익을 볼수 있을 것 같습니다.
http://www.xevious7.com/103 2006년 7월15일.
오래전에 점프나 포탄의 움직을 컴퓨터화면에 표시하기 위해서 직관적인 방법으로
사용했던 알고리즘을 한번 수학적으로 생각해보고 정리한 문서입니다.
직관적인 생각의 전개는 http://www.xevious7.com/102
에서 볼 수 있습니다. (즉 대략 직관적으로 저렇게 해도 비슷한 곡선이
나올것 같았고 실제로 해보니 그런곡선이 나오더라 에서 근데 왜 비슷한
곡선이 나오지 하고 이유를 생각해본 문서라고 할까요 ~)
이유를 생각해보니 단순하게 증분을 더하는 형태이고 .. 증분이 1일때
결국 1에서 n까지의 수열합으로 표시될 수 있었습니다.
즉 위의 방법은 n(n+1) / 2 의 형태의 운동방정식이 되는 것입니다.
그래서 생각한것이 그럼 일반 운동방정식 a * n^2 + c 형태의 방정식도 수열합이 가능하지
않을까 라고 생각해서보니 일반항이 2*n -1 인 수열의 합이 n^2 이므로 이것도 더하는
값만 n에서 2*n -1 으로 바뀐 똑같은 알고리즘 적용이 가능하다는 것까지 생각했습니다.

시간이 일정하고 시간의 값이 불변할때 이미 뉴튼에 의해서 이미 증명된 운동의방정식은
참입니다. 위의 글의 방법을 수열로 표현하면
즉 일정구간 (일정시간) T에 관한 거리는 각각 구간의 합으로 표현될 수 있다.
라는 것입니다.
좀더 이해를 이해서 풀어쓰면
T =1 일때 S1 = 1
T =2 일때 S2 = 1 + 2
T =3 일때 S3 = 1 + 2 + 3
T = n일때 Sn = 1 + 2 + 3 .... + n 이 됩니다.
이것은 일반항 An = n 인 수열의 합이 됩니다. 이 수열의 합은 수학교육과정에서
가장 먼저나오는 1에서 임의수 n까지의 정수합은 얼마인가? 라는 문제이고
알다시피 1/2 * n * (n + 1) 이며 이것은 2차방정식으로 운동의 방정식이 됩니다.
여기까지는 이미 대략적으로 전글에서도 알수 있는 것이지만 좀더 수학적으로
정리해보았습니다.
그런데 우리가 알고 있는 실제 운동의 방정식은 s = a * t ^2 의 꼴입니다.
위에서 2차 방정식이 수열의 합으로 표현하여 식을 간단히 했듯이 위의 운동방정식도
s값을 수열의 부분합이라고 생각하면 그 합이 n^2 이 된다고 생각할 수 있습니다.
다행히도 부분합이 n^2 을 가지는 수열은 잘 알려진 일반항이 An이 2n - 1 인
수열의 합이 됩니다.
이것을 이해하기 쉽게 풀어보면
T = 1 일때 S1 = 1
T = 2 일때 S2 = 4 = 1 + 3
T = 3 일때 S3 = 9 = 1 + 3 + 5
T = n 일때 Sn = n^2 = 1 + 3 + 5 + .... + 2n+1 이 됩니다.
자 이러면 우리가 현실세계의 사용하는 실제 운동의 방정식도 시간의 길이가 불변하는
일정구간 T에 대해서 곱을 사용하지하고 합을 사용하여 간략하게 표현할 수 있습니다.
즉 한번의 T구간에 대해서
거리는 부분합이므로
컴퓨터 알고리즘에서는 For 문에서 일반항만 계속 더하는 형태로
부분합을 구하면 그것이 바로 우리가 원하는 거리가 되는 것입니다.
즉 Tn 시점에서의 거리는 Tn-1 시점의 거리 + 일반항 이면 족합니다.
이렇게 미분방정식으로 수열로 생각하여 알고리즘을 구성하는 것은 여러응용에
훨씬 도움을 주리라고 생각합니다.
PS. 위의 방정식들을 보시다 시피 n(n+1)/2 나 n^2 의 기하학적인 곡선은 거의
동일하다고 생각할 수 있습니다. 왜냐면 n^2 를 1/2 로 스케일링 하면 큰 차이가
없는 곡선이 되는것입니다. 또한 그 곡선자체가 컴퓨터 그래픽에서 표현되는것이라면
사실상 무시해도 전혀 지장이 없습니다. 시뮬레이션이 아니라면 말이죠
따라서 1씩 증가하는 패턴의 공식으로 점프의 높이를 구현하는것이 속도상 조금의
이익을 볼수 있을 것 같습니다.